Nauka i religija >
Formula postojanja Boga
Naučnik iz Ohaja, Stefan D. Anvin, uspeo je da jednostavnim računom, koristeći poznatu Bajesovu teoremu iz statistike, odredi kako je verovatnoća postojanja Boga 67 odsto

Da li moderne, prirodne nauke mogu utvrditi postojanje Boga? Ovo je jedno od nezaobilaznih glupih pitanja koje će – u nedostatku svakodnevnih tema za razgovor – verovatno biti postavljeno fizičaru, hemičaru ili nekom drugom naučnom radniku, ako se ovaj slučajno zatekne u društvu radoznalaca ne-naučnika, sklonih nezahvalnoj raboti razmišljanja o krajnjim pitanjima. Možda bi se očekivalo da će savremeni naučnik bez mnogo razmišljanja odgovoriti kako je nauka odavno dokazala da Bog ne postoji i potom se vratiti nemilim mu svakodnevnim temama, ali to se neće neizostavno desiti. Kada ga, i ako – prođe faza mrštenja, kolutanja očima i drugih facijalnih reakcija na jedno "glupo" pitanje, savremeni naučni radnik, ako dobro razmisli, uglavnom će reći kako se iz perspektive samih prirodnih nauka ne može dati ni potvrdan ni odrečan odgovor o postojanju Boga. Mada je baš ovakav odgovor za okupljene radoznale sagovornike obično neočekivan, on baš i nije tekovina najsvežijih naučnih pregnuća. Grčki filozof Protagora (485–410. godine p.n.e.), jedan od prvih i najpoznatijih sofista, izrekao je još pre 2500 godina da "kada su bogovi u pitanju, ja ne mogu znati ni da li postoje, ni da li ne postoje, niti kakav je njihov oblik". Možda je razočaravajuće kako, dva i po milenijuma kasnije, uz sve uspehe savremenih nauka, moderni mislioci nisu odmakli ni korak od samoukog učitelja mudrosti iz Abdere. To je tako iz prostog razloga što se moderne, egzaktne nauke, prema predmetu svojih istraživanja i fokusu interesovanja, problemom postojanja Boga uopšte ne bave, niti su se tim, teološkim i čisto metafizičkim pitanjem ikada i bavile, bar otkako su – posle rođenja moderne fizike sa Galileom Galilejem i nesrećnog slučaja sa Đordanom Brunom – postale moderne i egzaktne. Osim što su pojedine zablude i bizarne mistifikacije prirodnih pojava, proklijale pod opskurnim okriljem religije, sa razvojem nauke dobile svoje pravo objašnjenje, uopšte nije tačna široko rasprostranjena predrasuda da je nauka, ničeovski grubo rečeno "ubila Boga", jer se fizika i teologija, u najmanju ruku, nalaze na mimoilaznim putanjama, svaka sa svojom mukom. Ako se pitamo ko je zapravo do "umiranja Boga" doveo, otvaramo mnoge druge, smrtno ozbiljne teme, ali – nauka, sama po sebi, nije. Isto tako, krajnje je neosnovano često pominjano tumačenje da naučna saznanja zapravo potvrđuju postojanje Boga samo zato što su utemeljivači fizike XX veka – Albert Ajnštajn, Maks Plank, Maks Born i mnogi drugi – privatno bili religiozni. Bilo čiji lični stav, bez obzira na njegovu genijalnost, o bilo kom pitanju nikako ne može biti uzet kao relevantan rezultat jedne egzaktne, eksperimentalne i matematičke nauke.
STATISTIČKI METOD: S druge strane, izvestan broj ozbiljnih pokušaja da se nauka i religija donekle povežu ipak postoji. O tome najbolje svedoči postojanje prestižne Templtonove nagrade koja se jednom godišnje dodeljuje uglednim naučnicima i teolozima za "napredak u religiji". Poslednjih godina, pod napretkom religiozne misli uglavnom su se podrazmevali nekoliki dostojni pokušaji teološke interpretacije zamršenih rezultata fizike elementarnih čestica i kosmologije, među kojima je u tom pogledu najpoznatiji antropički princip (verovanje da je, od Velikog praska naovamo, od svih mogućih univerzuma nastao baš onaj u kome se mogao razviti inteligentni život). Međutim, čak i pojedini stručnjaci koji istražuju moguće veze nauke i religije – što teolozi, što fizičari – ne misle da je opravdano očekivanje kako se pomoću antropičkog principa, inteligentnog dizajna vasione i sličnih hipoteza mogu dobiti odgovori na ultimativno pitanje o postojanju Boga. Fizičar iz Ohaja, doktor Stefan Anvin (Stephen D. Unwin), koji se do sada bavio istraživanjem kvantne gravitacije i statističkom analizom upravljanja rizicima, smatra da takav put, kao što je rekao Protagora, ne vodi ka potvrdnom, ali ni ka odrečnom odgovoru. Zato – umesto dosadašnjih pokušaja da se na osnovu složenih kosmoloških teorija savremene fizike ispita pitanje Boga – u svojoj vrlo zapaženoj knjizi Verovatnoća Boga, Stefan Anvin predlaže jedan sasvim novi, statistički metod, koji je baziran na Bajesovoj teoremi i toliko jednostavan da se može nazvati genijalnim. On uzima da početna verovatnoća postojanja Boga, pre bilo kakvih dokaza, iznosi Ppre=50 odsto (podjednaka verovatnoća da Bog postoji, ali i da ne postoji). Zatim primenjuje, za ovu priliku modifikovanu, Bajesovu formulu:
Pposle = Ppre x D / Ppre x D + 100% - Ppre
kako bi, na osnovu verovatnoće pre uvođenja dokaza božanskog postojanja, Ppre, dobio kolika je verovatnoća posle božanskog dokaza, koja je na levoj strani formule označena kao Pposle. Potom, ovaj račun ponavlja za šest različitih dokaza, tako što za svaki od šest parametra D, prethodno dobijenu verovatnoću Pposle ponovo unosi u Bajesovu formulu, ali sada na mestu Ppre. Inače, veličina D, takozvani božanski indikator, samo je veza između pretpostavke o postojanju samog Boga i pretpostavke o postojanju dokaza Boga, tj. božanske manifestacije. D-indikator matematički odgovara uslovnoj verovatnoći: kada bi Bog postojao, tada bi bilo D puta verovatnije da će se javiti i odgovarajući dokaz. U svom računu Anvin koristi šest vrednosti D-indikatora: priznanje dobrote (D=10, što znači da kada bi Bog postojao, priznanje dobrote bi bilo 10 puta verovatnije), postojanje moralnog zla (D=0,5), postojanje prirodnog zla (D=0,1), psihološka čuda – molitve (D=2), natprirodna čuda – vaskrsnuće (D=1) i religiozna iskustva (D=2). Zamenjujući odgovarajuće vrednosti u Bajesovoj formuli, tokom šest iteracija, Anvin dobija verovatnoću Božjeg postojanja. Kao što svako može da proveri u jednostavnom računu, za ovako izabrane vrednosti D-indikatora izračunava se da je verovatnoća da Bog postoji 67 odsto (tačnije, 66,666...odsto). Dakle, Bog je prilično, zapravo dvotrećinski, verovatan.
SUBJEKTIVNOST: Osnova Anvinove ideje počiva u inverziji teoloških koncepata. Umesto da postojanje Boga opravdava traženjem njegovih manifestacija, on na bazi složenih teoloških znanja, određuje koliko bi manifestacije bile očekivane ako bi se pretpostavilo da Bog postoji (procena vrednosti D-indikatora). Zatim, pomoću Bajesove teoreme lako izračunava inverznu verovatnoću: da postoji sam Bog, nezavisno od njegovih manifestacija. Pritom, uopšte nije neophodno da uranja u svu kompleksnost teologije i da utvrdi istinitost samih dokaza i manifestacija božanskog postojanja, već je dovoljno samo da poznaje koliko su te manifestacije verovatne kada se već pretpostavi da Bog postoji. Jednostavno i nedvosmisleno, utemeljeno na elementarnoj statistici – to rezultat od 67 odsto za postojanje Boga čini posebno privlačnim. Stoga su reakcije u naučnoj zajednici, ali i u široj javnosti, brojne i uglavnom pohvalne, dok su pojedini stručnjaci dočekali Anvinovu statističku procenu s velikim i neskrivenim oduševljenjem. Tako Pol Dejvis, lauerat Templtonove nagrade za 1999. godinu, smatra da je Stefan Anvin postigao praktično nemoguće uz pomoć minimalnog matematičkog proračuna, izbegavajući pritom da uplovi u opskurnost teoloških spekulacija. Međutim, dobijenu vrednost od 67 odsto ne treba shvatiti kao definitivno određenu verovatnoću za postojanje Boga ili kao kakvu fundamentalnu konstantu. Sam autor ističe da njegov proračun možda jeste omogućio da se prvi put izračuna verovatnoća postojanja Boga, ali se nikako ne bi mogao uporediti sa poduhvatom kao što je prvo izračunavanje broja Pi. Razlog za to je što izbor vrednosti D-indikatora predstavlja subjektivni element u proračunu, pošto je u krajnjoj liniji zasnovan na ličnoj proceni. Poznati kolumnista naučnog časopisa "Sajentifik Ameriken", Majkl Šermer, skreće posebnu pažnju na ovaj detalj. Koristeći identičan statistički metod i početnu pretpostavku o 50% odsto, Šermer ponavlja Anvinov račun, ali s drugačijim vrednostima D-indikatora, zasnovanim na svojoj studiji evolutivnog porekla morala i sociokulturnom poreklu vere: priznanje dobrote (D=0,5), postojanje moralnog zla (D=0,1), postojanje prirodnog zla (D=0,1), psihološka čuda (D=1), natprirodna čuda (D=0,5) i religiozna iskustva (D=0,1). Uz ove vrednosti D-indikatora, procenjenih sa najvećim mogućim skepticizmom, mogućnost da Bog postoji je svega 2 odsto. Šermer, doduše, ne insistira na ovako dobijenom rezultatu, ali ističe da on pokazuje kako Anvinova studija, matematički sasvim relevantna, zbog neizbežne subjektivnosti u određivanju verovatnoće nije mnogo više od zanimljive etide u razmišljanju, koja je prihvatljiva samo onima koji na neki način već veruju. Za sve ateiste i skeptike, ipak, nije došlo do presudnog razotkrivanja, pošto odgovor nije stigao samo kroz statistiku i logiku. Pitanje Boga ostalo je pitanje ličnog opredeljenja – pa tako i dalje izvan nauke. Religiozna istina je, očigledno, pre svega stvar ljudskih ubeđenja, uprkos svim pokušajima da se do nje dopre drugim sredstvima, što nas vraća na jednu drugu, verovatno poznatiju misao drevnog sofiste Protagore – "čovek je mera svih stvari". Očigledno, među svim tim stvarima, sa određenom verovatnoćom (bila ona 0, 2 ili 67 odsto), nalazi se i Bog.
Bajesova teorema
Bajesova teorema je jedno od elementarnih, ali za prirodne nauke vrlo korisnih, statističkih oruđa. Dobila je ime po engleskom svešteniku i matematičaru Tomasu Bajesu, koji je još u XVIII veku dao značajan doprinos razvoju matematičke statistike. Čitaocima "Vremena" kojima su osnove statističkog računa iz srednje škole i dalje u sećanju, bez sumnje je poznato da oznaka P(A) u statistici obično predstavlja verovatnoću događaja A, dok je, recimo, P(B) verovatnoća da se dogodi događaj B. Pored ovih, običnih verovatnoća, u statistici se koriste i takozvane uslovne verovatnoće, o kojima i govori Bajesova teorema. Tako je P(A|B) verovatnoća da se dogodi događaj A, ako se dogodio događaj B, što je u mnogim eksperimentima i teorijama (među ostalima, i u Anvinovoj računici božanske verovatnoće) vrlo značajna veličina za određivanje. Ponekad je, sticajem okolnosti, lakše izračunati inverznu uslovnu verovatnoću, P(B|A), tj. verovatnoću da se dogodi B ako se dogodio A, pa na osnovu nje odrediti P(A|B). Za to izračunavanje jedne uslovne verovatnoće na osnovu njoj inverzne služi formula Bajesove teoreme:
P(A/B) = ( P(A) x P(B/A) ) / ( P(A) x P(B/A) + P (AC) x P(B/AC)
Kao što se vidi, u brojiocu razlomka javlja se proizvod obične P(A) i uslovne verovatnoće P(B|A) (takav proizvod odgovara uslovu da su se dogodili i A i B), dok se u imeniocu pojavljuje zbir dva takva proizvoda. Oznaka AC predstavlja takozvani komplementaran događaj od A, a P(AC) verovatnoću da se dogodio AC, tj. da se sam A nije dogodio. Očigledno je da važi P(A)=100%-P(AC), jer je 100 odsto verovatnoća sigurnog događaja. Kako su A i AC dva nezavisna događaja i to takva da pokrivaju sve moguće događaje (ili se A dogodio ili se pak, nije dogodio, kada se zapravo dogodio AC), suma u imeniocu Bajesove formule odgovara verovatnoći da se B svakako dogodio, bez obzira na A. Treba napomenuti da se sumiranje u imeniocu Bajesove formule ne mora zaustaviti samo na dva moguća slučaja A i AC, kako je ovde zbog jednostavnosti dato, već se u opštem obliku suma zadaje preko više nezavisnih, međusobno isključujućih događaja A1, A2,... ,An.
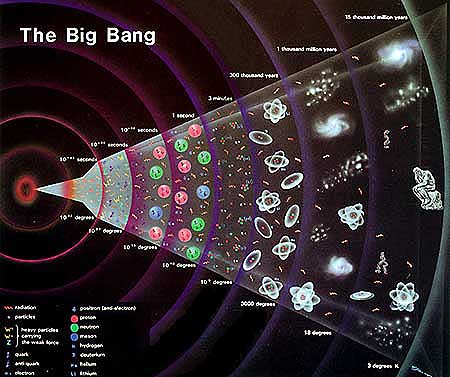
Legenda, počev od gornjeg levog simbola: radiation, particles, heavy particles, carrying, the weak force, quark, anti quark, electron, positron (anti-electron), proton, neutron, meson, hydrogen, deuterium, helium, lithium
 POŠALJI KOMENTAR REDAKCIJI
POŠALJI KOMENTAR REDAKCIJI
|  |
 ODŠTAMPAJ TEKST
ODŠTAMPAJ TEKST
|
|||
 | |||||
|
| |||||