Vreme nauke >

Dvadeset tri

Koliko je dovoljno za veštačku inteligenciju? Recimo da na Tjuringovom testu postavite ovo pitanje čoveku i mašini koji se znoje i razmišljaju u različitim sobama. Ako jedan odgovori 23, a drugi ne, ko je čovek, a ko veštačka inteligencija? I, zašto baš 23? Uz malo truda i pameti, može se iskopati takozvani numerološki značaj bilo kog broja za bilo koju pojavu, a naročito za 23. Naime, ovaj broj ima tu nesreću, ili "enigmu", da mu numerolozi i pseudonaučnici pripisuju kako je većina nesrećnih slučajeva na neki način povezana sa njim. Na primer, čovek je poginuo tačno 23 godine nakon što je doživeo prethodnu saobraćajnu nesreću, ili, pao je avion u kome je bila stjuardesa čija se sestra udala za čoveka koji je odgajio 23 legla mačića. Gotovo da nema slučaja gde se ne može naći slična veza sa bilo kojim brojem. Deluje kao sumanut sport, ali to nam sa raznim vezama i raznim brojevima svakodnevno rade.

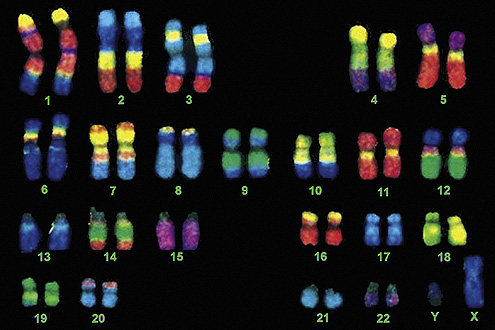
Međutim, neka se značenja zaista mogu učitati u broj 23. Prost račun verovatnoće, na primer, pokazuje da ako se u nekoj prostoriji nađe 23 osobe, verovatnoća da u njoj budu dve osobe sa istim datumom rođenja iznosi 50 odsto. Sa druge strane, u ljudskom organizmu svaka ćelija u svom jedru ima 23 para hromozoma (od kojih su 22 autozoma i jedan par polnih hromozoma X i Y). Takođe, broj 23 je red veličine Avogardovog broja, što će reći da u svakom molu nekog gasa uvek ima 1023 čestica.

Za matematiku je, naravno, zanimljiv jer je prost broj i kao takav, ima svakojake karakteristike u teoriji brojeva. Neke od onih monstruozno teških, nedokazivih teorema vezuju se i za njega, kao uostalom i za sve ostale proste brojeve. Slavan je slučaj kad je Dejvid Hilbert 1900. godine na kongresu matematičara u Parizu izneo listu svih takvih nerešenih matematičkih problema – bilo ih je tačno 23. Neki od njih kao Velika Fermaova teorema ili Poenkareova hipoteza su kasnije uspešno rešeni. No, najdramatičniji odgovor stigao je 1930. od Kurta Gedela, koji je za prva dva pitanja iz ovog problema dokazao da se ne može znati jesu li te teoreme uopšte dokazive i da se, zapravo, ne može napraviti zatvorena matematička teorija.

To je za matematičare bio nesrećan slučaj, jednako tragičan kao pomenuto padanje aviona ili drugih udesa. Ali, to nije bilo sve. Sedam godina kasnije, odgovarajući takođe negativno na treći deo ovog Hilbertovog problema, Alan Tjuring je konstruisao zamišljenu Tjuringovu mašinu, bez koje zapravo nikad ne bi bilo ni računara, ni potencijalne veštačke inteligencije. Savremena tehnološka revolucija je počela ovde, u prostoru najčistije, formalne matematike.

Međutim, kako kaže ser Rodžer Penrouz u "Carevom novom umu", Gedelova teorema je i pre Tjuringa postavila suštinska ograničenja – ako sve tačne iskaze ne može dokazati nijedan formalni sistem, onda to ne može niti jedan kompjuterski program (koji je i sam formalni sistem).

Da li je 23 neophodno za veštačku inteligenciju? Mašina će uvek odgovoriti da jeste, ma koliko simulirala da je čovek – negativan odgovor dovodi u pitanje samu njenu pretpostavku da jeste veštački inteligentna. Bez obzira na 23. Čovek ga, međutim, neće ignorisati.

 

POŠALJI KOMENTAR REDAKCIJI		ODŠTAMPAJ TEKST

---